Strips Planning Systems -Backward Search Method
- In order to make a backward search we must start from goal wffs.
- After starting from goal wffs we go back through STRIPS rule so that sub-goal wff is produced.
- If the goal wff formula is g if we go back from g through a STRIPS rule β we get a formula which is weaker that is g' which is the sub-goal.
- If g' is satisfied before applying the instance of β, the goal wff g will be. satisfied after the instance of β is applied.
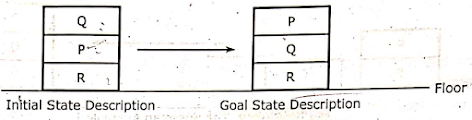
- Let us explain with an example by taking the goal state as P on Q on R which are on floor from the initial state description as Q is on P, P is on R, R on floor which can be seen from Fig. 3.10.4.
Fig. 3.10.4 A State Description
- The goal wff is,
On(R, F) ∧ On(Q, R) ∧ On(P, Q)
- Now we have to use any operation to the-goal condition so that one of conjuncts in goal condition are achieved.
- So first we use move(P, x, Q) to get a sub-goal wff.
- We take variable 'x' because P has to moved from some where to Q.
- The preconditions that should exist for the operator to apply are,
On(P, x)
Clear(P)
Clear(Q).
- By using the operation move (P, X, Q) one of the conjunct of goal wff i.e., On(P, Q) is achieved.
- On(P, Q) may not be present in the sub-goal, but the preconditions which are not present in the goal wff has to be present in it.
- The variable 'x' cannot be I as P is being moved onto Q, it cannot be Q as it is to which it is being moved, it cannot be R, if it is R On(P, R) has to be in sub-goal wff so we can't achieve On(Q, R). So we consider x to be floor move(P, x, Q) is known to be partially instantiated operator as x is not known.
- Another approach for backward search is to use move(Q, z, R) to achieve On(Q, R).
- The preconditions are,
On(Q, z)
Clear(Q)
Clear(R)
Here z cannot be P as it On(Q, P) is not mentioned in goal state, it cannot be Q as it is being moved and it cannot be R as we are moving to it. So here also it is assumed to be floor.
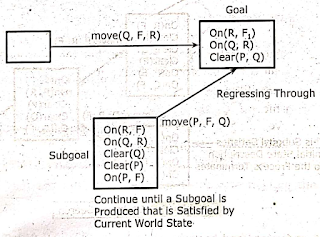
- The result of regression through move(P, x, Q) is shown in Fig. 3.10.5.
Fig. 3.10.5 Regressing a Conjunction through STRIPS Rule Containing Variables
- It has to be noted the other sub-goal wffs that are not produced are neither added nor destroyed by the operator so they are simply passed through the operator.
- Delaying the specification, of 'from place' in move operator is known as least commitment planning.
- It the from place' is floor the operation will become move(P, F, Q) and On(P, Q) is achieved. The Fig. 3.10.6 represents the regression through move(P, F, Q).
Fig:3.10.6 Regressing a Conjunction through STRIPS Operator
- The backward search continues until a sub-goal is produced that satisfies the initial state description..
- In large problems the occurrence of variables may complicate the backward search procedure.
- The complete procedure of backward search for the example in Fig. 3.10.4 can be shown in the Fig. 3..10.7.
Fig. 3.10.7 Backward Search
- In breadth first forward and backward search, no particular order is followed in order to achieve goal conjuncts.
- It is beneficial to search in plan space instead of searching in formula spaces. Partial ordering of steps can be observed in plan spaces.