Frame Axioms

Some Difficulties 

Frame Axioms 

• The effect axioms do not infer all the statements which are true about a state after, the action.
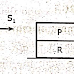
• For example, consider the Fig. 3.9.3

Fig. 3.9.3: Mapping state-action pair into state

• On performing do move(Q, P, F), S₀), S₁ is reached. 
• The inferences using effect axioms are, 

                On(Q, F, do(move(Q, P, F), S₀)) 

                ᆨOn(Q, P, do(move(Q, P, F), S₀) 

                Clear(P, do(move(Q, P, F), S₀)). 

• These inferences do not state the facts which are true after performing action like P is on R, R is on floor and Q is clear.
• To infer such constants which are true frame axioms are used.
• The frame axiom inferences from the figure are,

                        On(P, R, do(move(Q, P, F),,S₀))

                        On(R, F, do(move(Q, P, F), S₀)) 

                        Clear(Q, do(move(Q, P, F), S₀)) 

• Let us take an example, to represent the frame axioms for {move, On} pair, 

                    [On(x, y, s) ∧ (x ≠ u)] ⊃ On(x, y, do(move(u, v, z), s)]. 

    It represents that x is on y which is true after the action is performed to move u onto z which does not move x. This is a positive frame axiom, 

                    ᆨOn(x, y, s) ∧ [(x  ≠ u) ∨ (y  ≠ z)] 

                    ⊃ᆨOn(x, y, do(move(u, v, z), s)) 

    It is a negative frame axiom which states that if x is not on the y before action, it is still not on y after the action is performed if the action does not place it on y. 

• The main idea of frame axioms is to prove that a property of a state does not change if the action performed on the state does not affect that property. 
• It becomes difficult to manage to represent the changes because each fluent and action has a pair of frame axioms, which results in a large number of frame axioms. 
• It needs to reduce the frame axioms, but if the frame axioms are reduced it becomes difficult to represent the fluents which does not change over a sequence of actions performed. 
• This problem of dealing with fluents which does not change when actions are performed is called frame problem.

Qualifications

• The transition formula of move has an antecedent which describes the conditions that are to be present before performing the action for a perfect case. 
• For example, if we want that is to be moved is not tempered then this condition has to be added to the antecedent, that is ᆨtempered(x) must be added to the conditions. 
• The conditions like not tampered are called qualifications.
• There may be many qualifications which we want to add to the antecedent. 
• It is not easy to represent all of the qualifications which are important, this problem of representing all the qualifications is called qualification problem. 
• Non monotonic reasoning is used to deal with the qualification problem but it is not fully successful.

Ramifications

• It is a problem which is concerned with indirect consequences of actions 
• It is might be posed as how to represent what happens implicitly due to an action, or to control secondary on tertiary effects with in a same period. It is strongly connected to, and is opposite of the qualification side of frame problem. 
• For example, if a person carrying an object may conclude the object is in the room in which he is present. 
• That is if we know location of person we obviously know the location of object.
• If initially the object is in room 1 i.e. In(O, R1) after moving to other room In(O, R2) it can be concluded by using effect axioms that the person is also present in new situation. This is indirect consequence. 
• The frame axioms which concludes the package is not in room 1 have to be prevented. 
• In order to prevent frame axioms a track should be maintained about which derived formulas survive the subsequent state transitions. This is known as ramification problem. 

Generating Plans

• The plan to achieve goal state is generated by temporarily ignoring frame, qualification and ramification problems. 
• Let the goal be g(s) then we have to prove that their exists a state s that is g(s) i.e. denoted by (∃s) g(s). 
• Example: Suppose, that we want a plan which places Q on the floor F in the Fig. 4.1.1 from the state S₀. In order to know the plan we have to prove (∃s) On(Q, F, S). 

        We have the formulas, 

                On(Q, P, S₀) 

                On(P, R, S₀) 

                On(R, F, S₀) 

                Clear(Q, S₀) 

                Clear(F, S₀) 

                [On(x, y, s) ∧ Clear(x, s) ∧ Clear(z, s) ∧ (x ≠ z) ⊃On(x, z, do(move(x, y, z), s))] is the positive effect axiom for{On, move}

• By chaining example goal would be true if we could prove, 

                On(Q, P, S) ∧ Clear(Q, S) ∧ Clear (F, S) ∧ (Q ≠ F) is true. 

• As all of them are true it implies On(Q, F, do(move(Q, P, F), is is true. 
• So, as the only action we could see is do(move(Q, P, F)) which is executed in situation or state S₀, so this is our plan. 
• We would get the plan as (do(move(P, R, Q), do(move(Q, P, .F), S₀)) if we have to get block P onto Q. The proof for these type of plan many become complex.